ALGEBRA, TEORIA DE NUMEROS Y GEOMETRÍA

ALGEBRA, TEORIA DE NUMEROS Y GEOMETRÍA

TEOREMA FUNDAMENTAL DEL ALGEBRA

FTA: Cada ecuación polinómica de grado n, con coeficientes complejos, tiene n raíces en el cuerpo de los complejos. (Todo polinomio con coeficientes reales o complejos tiene por lo menos una raiz real o compleja).

De hecho existen muchas formulaciones equivalentes del FTA. Por ejemplo, que cada polinomio real puede ser expresado como producto de factores lineales reales o cudráticos reales.

Demostraciones del Teorema Fundamental por Jean Le Rond d'Alembert

En 1746, D'Alembert hizo el primer intento serio de demostración del FTA. Para un polinomio f, tomó dos números reales b, c tal que f(b) = c. Entonces, demostró que existen dos complejos z1 y w1 tal que |z1| < |c|, |w1| < |c| y f(z1)=w1. Entonces, itera el proceso para converger a una raíz de f. Su demostración tenía varias debilidades. En primer lugar, usa un lema sin demostración que no fue demostrado hasta 1851, por Puiseau, pero ¡cuya demostración usa el FTA!. En segundo lugar, no usó ningún criterio de compacidad para la existencia de la convergencia. No obstante, las ideas de la esta demostración son importantes.

EL INTENTO DE ALEMBERT

D'Alembert establece una demostración esquemática del TFA. De esta manera, plantea que cualquier polinomio, el cual está en términos de 𝑦, se puede factorizar cuando el grado del polinomio es par, como en el caso de 𝑦𝑦 + 𝑓𝑦 + 𝑔, 𝑦𝑦 + ℎ𝑦 + 𝑖, etc. donde todos sus coeficientes: 𝑓, 𝑔, ℎ, 𝑙, etc. son reales, pues para 𝑦𝑦 + 𝑓𝑦 + 𝑔 se tiene que si 𝑎 es una raíz real, siempre hay una segunda 𝑏, la cual también será real y el producto:

(𝑦 − 𝑎)(𝑦 − 𝑏) = 𝑦𝑦 + 𝑓𝑦 + 𝑔.

Por otro lado, desde Newton se sabía que las raíces complejas de una ecuación polinómica vienen en pares conjugados. Además, si se multiplica un número complejo por su conjugado, su producto es un polinomio real. D'Alembert también menciona que un polinomio siempre se puede dividir en factores 𝑦𝑦 + ℎ𝑦 + 𝑖, 𝑦𝑦 + ℎ𝑦 + 𝑚, etc., con coeficientes reales. Es decir que un polinomio se puede descomponer en factores cuadráticos reales, lo cual da respuesta a una de las preguntas que Leibniz se había planteado tiempo atrás.

Demostraciones del Teorema Fundamental por Euler

Al poco tiempo, Euler fue capaz de probar que todo polinomio real con grado, n < 7, tiene exactamente n raíces complejas. En 1749, intentó una demostración del caso general, o sea, el FTA para polinomios reales. Su demostración, que aparece en Recherches sur les racines imaginaires des équations, está basada en descomponer un polinomio mónico reducido (con a_{n-1}=0), de grado n=2^r, en el producto de dos polinomios mónicos de grados iguales, 2^{r-1}. Multiplicando posiblemente el polinomio inicial por un factor de la forma ax^k y aplicando después un cambio lineal para convertirlo en uno mónico reducido y de grado potencia de dos. Ya en el Ars Magna de Cardano aparece el cambio de variable para hacer cero el coeficiente de la segunda potencia mas grande de la indetrerminada. O sea, en descomponer un polinomio mónico de grado 2n en dos de grados m = 2n-1. Suponiendo que

x^{2m} + Ax^{2m-2} + Bx^{2m-3} +. . . = (x^m + tx^{m-1} + gx^{m-2} + . . .)(x^m - tx^{m-1} + hx^{m-2} + . . .)

y entonces multiplica en el segundo miembro e iguala coeficientes. Euler afirmó que esto conduce a obtener los coeficientes g, h, ... como funciones racionales de los coeficientes originales A, B,... Esto lo realizó paea n = 4, pero esquematizó el caso general.

El intento de Euler

Para su versión del TFA, Euler parte de tres principios, los cuales son aceptados por él sin demostración alguna. Estos enuncian lo siguiente:

i. la posibilidad de factorizar un polinomio en factores lineales,

ii. el número de raíces es igual al grado de la ecuación, deducido de (i).

iii. las relaciones entre coeficientes y raíces, deducidas también de (i), mediante un cálculo

de las raíces como si se tratase de números ordinarios.

EULER Y LA TEORÍA DE NÚMEROS

El interés de Euler en la teoría de números procede de la influencia de Christian Goldbach, amigo suyo durante su estancia en la Academia de San Petersburgo. Gran parte de los primeros trabajos de Euler en teoría de números se basan en los trabajos de Pierre de Fermat. Euler desarrolló algunas de las ideas de este matemático francés pero descartó también algunas de sus conjeturas.

Euler unió la naturaleza de la distribución de los números primos con sus ideas del análisis matemático.

 · Demostró el pequeño teorema de Fermat

· Generalizó el pequeño teorema de Fermat a lo que se conoce como el teorema de Euler

 · Definió la función φ de Euler

· Contribuyó de manera significativa al entendimiento de los números perfectos

· Y avanzó en la investigación de lo que más tarde se concretaría en el teorema de los números primos. Demostró la divergencia de la suma de los inversos de los números primos y, al hacerlo, descubrió la conexión entre la función zeta de Riemann y los números primos.

CONGRUENCIA DE EULER

Sea φ(n) = #{1 ≤ m ≤ n : mcd(m, n) = 1}, entonces para a y n coprimos se cumple a φ(n) ≡ 1 (mod n). La demostración de la congruencia de Euler-Fermat hoy en día se reduce a notar que el orden de cualquier elemento del grupo multiplicativo Z ∗ n debe dividir al orden del grupo, que es φ(n). Por supuesto, Euler no podía apelar a este resultado pero en cierta forma su demostración se basa en la idea de la partición en cogrupos [Su], [Di].

LA GEOMETRÍA EN EL SIGLO VXIII - EL QUINTO POSTULADO DE EUCLIDES

Aunque el énfasis en la matemática a partir de 1650 estaba puesto cada vez más en el análisis, las preguntas fundamentales de la geometría clásica continuaron despertando interés. La atención se centró en el quinto postulado del Libro I de los Elementos, que Euclides había utilizado para probar la existencia de una única paralela a través de un punto a una recta dada. Desde la antigüedad, geómetras griegos, islámicos y europeos habían intentado, sin éxito, demostrar que el postulado de las paralelas no tiene por qué ser un postulado, sino que podía deducirse de los otros postulados de la geometría euclidiana. Durante el período entre 1600 y 1800, los matemáticos continuaron estos esfuerzos por tratar de demostrar que el postulado era equivalente a algún resultado que fuera considerado evidente por sí mismo. Aunque el avance decisivo en la geometría no euclidiana no ocurriría hasta el siglo XIX, los investigadores lograron un entendimiento más profundo y sistemático de las propiedades clásicas del espacio.

El interés por el postulado de las paralelas se desarrolló en el siglo XVI después de la recuperación y traducción al latin del comentario de Proclo sobre los Elementosde Euclides. Los investigadores italianos Christopher Clavius en 1574 y Giordano Vitale en 1680 mostraron que el postulado es equivalente a afirmar que la línea equidistante a una recta es una línea recta. En 1693 John Wallis, profesor savilian de geometría en Oxford, intentó una demostración diferente, probando que el axioma se sigue de la hipótesis de que a cada figura existe una figura semejante de magnitud arbitraria.

Christopher Clavius

En 1733 el italiano Girolamo Saccheri publicó su Euclides ab Omni Naevo Vindicatus (“Euclides Borrado de todos los defectos”). Este fue un importante trabajo de síntesis en el que proporciona un análisis completo del problema de las paralelas en términos de los cuadriláteros de Omar Khayyam. Utilizando el supuesto euclidiano de que las líneas rectas no encierran un área, fue capaz de excluir a las geometrías que no contienen paralelas. Queda por demostrar la existencia de una única paralela a través de un punto a una recta dada. Para ello, Saccheri adoptó el procedimiento de reducción al absurdo. Supuso la existencia de más de un paralela y trató de derivar una contradicción. Después de una investigación larga y detallada, fue capaz de convencerse a sí mismo (erróneamente) que había encontrado la contradicción deseada.

En 1766 Johann Heinrich Lambert de la Academia de Berlín compuso Die Theorie der Parallellinien ( “La Teoría de líneas paralelas”, publicado en 1786), un estudio penetrante del quinto postulado de la geometría euclidiana. Entre otros teoremas Lambert demostró que el axioma de las paralelas es equivalente afirmar que la suma de los ángulos de un triángulo es igual a dos ángulos rectos. Combinó este hecho con el resultado de Wallis para llegar a una caracterización inesperada del espacio clásico. 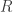De acuerdo con Lambert, si se rechaza el postulado de las paralelas, se deduce que para cada ángulo  es menor que  ( es un ángulo recto) se puede construir un triángulo equilátero con  ángulo en la esquina. Como consecuencia del resultado de Wallis cualquier triángulo semejante a este triángulo debe ser congruente a él. Por lo tanto, es posible asociar con cada ángulo de una longitud definida, el lado del triángulo equilátero correspondiente. Dado que la medición de ángulos es absoluta, independiente de cualquier convención relativa a la selección de unidades, se deduce que existe una unidad absoluta de longitud. Por lo tanto, aceptar el postulado de las paralelas es negar la posibilidad de un concepto absoluto de longitud.

Johann Heinrich Lambert

La contribución final del siglo XVIII a la teoría de las paralelas fue un libro de texto de Adrien-Marie Legendre titulado Éléments de géométrie (Elementos de Geometría y Trigonometría), cuya primera edición apareció en 1794. Legendre presentó una elegante demostración que pretendía demostrar que la suma de los ángulos de un triángulo es igual a dos ángulos rectos. Él creía que había establecido de manera concluyente la validez del postulado de las paralelas. Su trabajo atrajo a una gran audiencia y fue influyente al informar a los lectores las nuevas ideas en la geometría.

El fracaso del siglo XVIII para desarrollar una geometría no euclidiana estaba arraigado en profundas creencias filosóficas. En su Crítica de la razón pura (1781) Emmanuel Kant había hecho hincapié en el carácter sintético a priori de los juicios matemáticos. Desde este punto de vista, las afirmaciones de la geometría y la aritmética son necesariamente proposiciones verdaderas con contenido empírico definido. La existencia de figuras semejantes de diferente tamaño, o el carácter convencional de las unidades de longitud, parecía evidente para los matemáticos de la época. Incluso en 1824 Pierre-Simon, marqués de Laplace, escribió:

Así, la noción de espacio incluye una propiedad especial, evidente por sí misma, sin la cual las propiedades de las paralelas no se pueden establecer de forma rigurosa. La idea de una región acotada, por ejemplo, el círculo, no contiene nada que depende de su magnitud absoluta. Pero si nos imaginamos su radio disminuyendo, somos llevados sin falta a la disminución en la misma proporción de su circunferencia y los lados de todas las figuras inscritas. Esta proporcionalidad se me aparece un postulado más natural que el de Euclides, y es digno de notar que se descubre de nuevo en los resultados de la teoría de la gravitación universal.

GEOMETRÍA SINTÉTICA

La geometría pura o sintética es una rama de las matemáticas, que se encarga de estudiar y construir de manera sintética las formas y lugares geométricos.

Se dice que la geometría pura o sintética es aquella que puedes construir axiomáticamente (con un sistema axiomático), con un tratamiento lógico-deductivo; es decir, a partir de una serie de axiomas o postulados (que se adopten a priori) se comienza a construir y demostrar proposiciones lógicas; que se sustentan como en una especie de eslabones de una cadena de razonamiento.

GEOMETRÍA ANALITICA

La geometría analítica estudia las lineas y figuras geométricas mediante la aplicación de técnicas básicas de álgebra y análisis matemático en un determinado sistema de coordenadas.

En consecuencia, la geometría analítica es una rama de las matemáticas que analiza en detalle todos los datos de las figuras geométricas, es decir, el volumen, los ángulos, el área, los puntos de intersección,  sus distancias, entre otros.

La característica fundamental de la geometría analítica es que permite la representación de las figuras geométricas a través de fórmulas.

Por ejemplo, las circunferencia son representadas por ecuaciones polinómicas de segundo grado mientras que las rectas son expresadas con ecuaciones polinómicas de primer grado.

APLICACIONES

Existen variadas aplicaciones de la geometría analítica en distintos ámbitos de la vida diaria. Por ejemplo, podemos encontrar la parábola, uno de los elementos fundamentales de la geometría analítica, en muchas de las herramientas que se utilizan cotidianamente en la actualidad. Algunas de estas herramientas son las siguientes: Antena parabólica, Puentes colgantes, Análisis astronómico, Telescopio Cassegrain.

DIFERENCIA ENTRE GEOMETRÍA SINTETICA Y ANALITICA

La mayor diferencia entre la geometría analítica y la geometría sintética, radica en el estudio y tratamiento que se les da a éstas, por ejemplo, en la geometría analítica el uso del álgebra, en especial el álgebra lineal, es fundamental, sin embargo, para la geometría pura no es tan indispensable el enfoque algebraico (sin que esto signifique su exclusión).